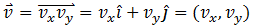Circle-Line Collision Tutorial

Research Paper

LISEF Poster

Source Code

Honorary Mention in Computer Science and Intel Award for Excellence in Computer Science from the 2010 Long Island Science and Engineering Fair (LISEF)

Presented at the Annual Research Association Science Fair at Jericho High School in 2010.

Introduction Object Definitions Line-Line Intersection The Closest Point on a Line to a Point Algorithm Collision Detection Static Circle and Static Line Segment Moving Circle and Static Line Segment Collision Response Conclusion External Links

Introduction

Collision detection and response between a moving circle and a static line segment in two dimensions is not an easy task. This algorithm in this tutorial is intended to accurately find the location of the collision and calculate the resultant velocity without using discrete time steps (moving the circle forward until a collision occurs). Thus the algorithm works with dynamic circles that respond to impulse forces. It is designed to use linear algebra in order to avoid using (relatively) computationally costly square roots, so some logic may seem quite roundabout.

This tutorial assumes basic knowledge of a programming language (Java in particular) and knowledge of basic algebra and geometry. Circles in this algorithm are assumed to be non-rotating.

Object Definitions
Moving circle (circle)
  • Initial position (x, y)
  • Velocity described by its components <u, v>
  • Radius r

The movement vector is <u,v>.

Static line segment (line)
  • Two endpoints, (x1, y1) and (x2, y2)

Line-Line Intersection

Finding the point of intersection between two line segments is crucial to the line-circle collision algorithm. This is done using Cramer's rule, matrices, and determinants, but can be simplified to simple algebra.

Steps

  1. Start with two line segments, one described by endpoints (x1, y1) and (x2, y2) and the other by (x3, y3) and (x4, y4).
  2. Take the endpoints of each of the line segments and turn it into an equation of the form Ax + By = C.
      
  3. Rearrange into a linear system of equations.
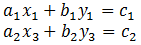
  4. Find the determinant of the two equations algebraically: determinant = A1 * B2 - A2 * B1.
  5. Use Cramer's Rule to solve for the point of intersection.

    If the determinant is zero, the lines are parallel or equal, and thus there is no point of intersection.

  6. Make sure the point of intersection is between the endpoints of the two line segments (or else only the infinite lines have intersected, which always occurs for non-parallel lines).

Java code

Point checklinescollide(float x1, float y1, float x2, float y2, 
                        float x3, float y3, float x4, float y4){
    float A1 = y2-y1;
    float B1 = x1-x2;
    float C1 = A1*x1 + B1*y1;
    float A2 = y4-y3;
    float B2 = x3-x4;
    float C2 = A2*x3 + B2*y3;
    float det = A1*B2-A2*B1;
    if(det != 0){
                float x = (B2*C1 - B1*C2)/det;
                float y = (A1*C2 - A2*C1)/det;
                if(x >= Math.min(x1, x2) && x <= Math.max(x1, x2) 
                                && x >= Math.min(x3, x4) && x <= Math.max(x3, x4)
                                && y >= Math.min(y1, y2) && y <= Math.max(y1, y2) 
                                && y >= Math.min(y3, y4) && y <= Math.max(y3, y4))
                        return new Point(x, y);
    }
    return null;
}

The Closest Point on a Line to a Point Algorithm

The closest point on a line to a point algorithm does exactly what its name says - it finds the closest point on the given line segment to the given point. It is an extension of the line-line intersection algorithm and is used to find when a collision occurs and where it occurs, and is quite critical to the line-circle collision detection algorithm.

Steps

  1. Start with a given point (x0, y0) and a given line segment, described by endpoints (lx1, ly1) and (lx2, ly2).
  2. Take the endpoints of the line segment and turn it into an equation of the form Ax + By = C.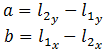
     
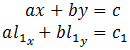
  3. The equation of the line perpendicular to the initial line segment is given by  -Bx + Ay = C, but this time (x, y) is the given point so that the new equation crosses through the given point.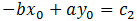
  4. Find the determinant of the two equations algebraically: determinant = A*A + B*B.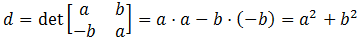
  5. Use Cramer's Rule to solve for the point of intersection of the original line and the perpendicular line, and that gives us the closest point on the given line to given point.
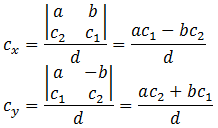    If the  determinant = 0 , then the point is on the line, and thus the closest point on the line to the point is the point itself!

Java Code

Point closestpointonline(float lx1, float ly1, 
      float lx2, float ly2, float x0, float y0){ 
      float A1 = ly2 - ly1; 
      float B1 = lx1 - lx2; 
      double C1 = (ly2 - ly1)*lx1 + (lx1 - lx2)*ly1; 
      double C2 = -B1*x0 + A1*y0; 
      double det = A1*A1 - -B1*B1; 
      double cx = 0; 
      double cy = 0; 
      if(det != 0){ 
            cx = (float)((A1*C1 - B1*C2)/det); 
            cy = (float)((A1*C2 - -B1*C1)/det); 
      }else{ 
            cx = x0; 
            cy = y0; 
      } 
      return new Point(cx, cy); 
}

Collision Detection

Collision detection is the process of detecting whether or not two objects have collided. We need to check if the circle has already collided with the line or if the circle will collide with the line before the end of the movement vector.

Note that distance refers to Euclidean distance, which is basically the Pythagorean theorem.

Static Circle and Static Line Segment

Applet failed to run. No Java plug-in was found.

Determine the distance from the circle to the line by first finding the closest point on the line to the center of the circle (point1) using the closest line on a point to a line algorithm.

  • If the distance from point1 to the center of the circle is zero, the circle is on the line. Make sure point1 is between the endpoints of the line.
  • If the distance from point1 to the center of the circle is less than r, the circle is touching the line. Make sure point1 is between the endpoints of the line.
  • If the distance from point1 to the center of the circle is greater than r, the circle is not touching the line, but the movement of the circle may cause a collision.

Moving Circle and Static Line Segment

Though continuous collision detection with dynamic circles is often complicated, this is mitigated by the fact that only the circle is moving, and thus only the position and velocity of the circle need to be considered.
 Find several other points:
  • The point of intersection between line and the movement vector of the circle. (a)
  • The closest point on the line to the endpoint of the movement vector of the circle. (b)
  • The closest point on the movement vector to (x1, y1). (c)
  • The closest point on the movement vector to the other endpoint. (d)
Using the points, it is then possible to eliminate many positions that would not result in a collision. A collision is possible if:
  • a is on the line and on the movement vector.
  • b is less than r away from the endpoint of the movement vector and on the line segment.
  • c is less than r away from (x1, y1) and on the movement vector.
  • d is less than r away from (x2, y2) and on the movement vector.
The circle's position at the time of collision (point2) can then be found using a similar triangle formed by point1, a, r (the circle's radius), and C (the center of the circle). This is described in the equation below:
v is the movement vector of the circle and C is the location of the circle.
The closest point on the line to point2, the point of contact between the circle and the line (pointC) can then be found. To determine the collision response algorithm to use:
  1. If pointC is on the line, then the closest point on the line shifted by r to the circle between the circle and the line is point3 = point2 + (point1 - pointC). This means that the circle has collided with the line, and point3 will be used later.
  2. If pointC is not on the line, then the circle has collided with an endpoint.
If the circle has collided with an endpoint, it becomes a subset of the moving circle - static circle collision problem, as long as we treat the endpoint as a static circle with zero radius:
  1. Find the distance to the closest point on the movement vector to the endpoint the circle collided with (d).
  2. Use the Pythagorean theorem to find x, the distance to move back along the movement vector.
  3. Move back along the movement vector to arrive at the location at the circle at the time of collision. 

Collision Response

Applet failed to run. No Java plug-in was found.
Since the line is static, no energy should be lost to the line (making the collision elastic) and the only part of the velocity that changes is the direction.

  • If the circle has collided with the line, then the direction the circle is heading just needs to be flipped over the line.

    1. A simple geometric manipulation gives us a new vector that contains the direction (but the wrong length): directionvector = circle - 2 * (point3 - point2) + point2
    2. Normalizing directionvector gives us the direction as a unit vector.
    3. Then multiplying directionvector by the length of the velocity gives the final post-collision velocity.

  • If the circle has collided with an endpoint, then the direction from the endpoint to the location of the circle at the point of collision is the new direction the circle is heading. This direction is represented by the vector r (not the distance) in the previous diagram. This algorithm is more fully explained in the circle - circle collision tutorial, since this is just a subset of the moving circle - static circle collision problem. The endpoint is simply treated as a circle of zero radius.

    1. Normalize the vector r: r/radius.
    2. Multiply the vector r by the length of the movement vector to get the final post-collision velocity.
Once the resultant velocity is found, the result may be scaled using the coefficient of restitution to simulate a loss in energy. This can be used to simulate sliding as seen in my force engine, my 2D Java physics engine (first lower the coefficient of restitution!).

Conclusion

Once collision detection and collision response are combined, you have a working line-circle collision simulation algorithm! Of course, this algorithm isn't perfect, because we treat the endpoints as circles with zero radii, but the errors that result aren't major. The problems are detailed more throughly in my paper.

External Links

Algorithm Tutorials - covers the line-line collision detection formula and more.

N Tutorial A - Collision Detection and Response - deals with rectangles and specialized shapes and has a useful appendix.

Pool Hall Lessons: Fast, Accurate Collision Detection Between Circles or Spheres - deals with circle-circle collision, which can be used to give thickness to the line.